El intervalo de confianza es una expresión estadística para determinar entre qué valores se sitúa la media de un conjunto de datos. Su aplicación práctica nos permite conocer, por ejemplo, entre qué dos valores oscila la durabilidad de unos neumáticos, o entre qué dos pesos se encuentra la población de un país.

Este cálculo también puede utilizarse para saber cuán estable es una medición que realizamos. Es decir, podremos conocer qué tan cerca está nuestra medición respecto al valor estimado original si repitiéramos nuestro experimento.

Dicho así resulta un poco abstracto, por lo que te lo explicaremos con algunos gráficos y ejemplos para ayudarte a comprenderlo.

Entremos en materia 

Si analizamos un gráfico de distribución normal, el intervalo de confianza representa toda el área bajo la curva que se ubica entre un valor mínimo y un valor máximo. Dichos valores se encuentran ubicados a igual distancia, pero en sentido contrario de la media (x̅). De ahí que la fórmula para calcular el intervalo de confianza se base en hallar esos valores.

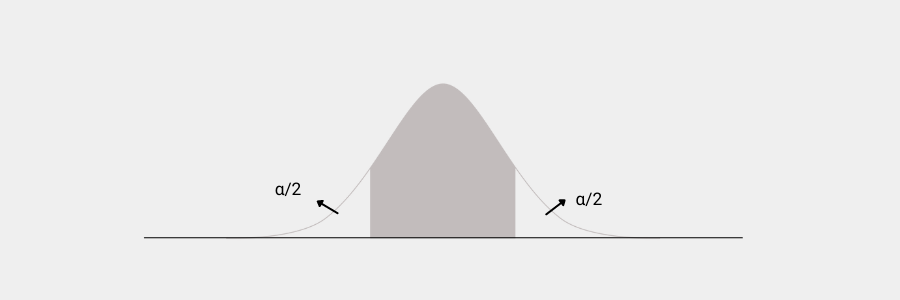
Fórmulas

Para calcular el valor mínimo y máximo del intervalo de confianza se utilizan las fórmulas:

 Valor mínimo = x̅ - Z_{α/2 -} (S / √n)

Valor máximo = x̅ + Z_{α/2 *} (S / √n)

 Si deseas expresar ambas fórmulas en una sola podrás hacerlo combinando las anteriores y empleando el signo de ±.

 <M> _1-α = x̅ ± Z_α/2 * (S / √n)

El resultado final contendrá dos valores: resultado de la suma; resultado de la resta. El menor de ambos indica el valor mínimo en el que comienza nuestro intervalo de confianza; mientras que el valor mayor pauta en el que acaba.

Visto así puede parecer complejo, pero es más sencillo de lo que parece. Empleamos elementos de colores que te ayudarán a relacionar visualmente cada parte de la fórmula del cálculo del intervalo de confianza.

Cómo calcular cada uno de los elementos

 1- ( x̅ ) Representa la media o promedio. Se calcula sumando todos los datos y dividiéndolos por la cantidad de datos (n).

 2- ( Z_α/2 ) Para calcular este valor debemos calcular primero el valor de _α y dividirlo entre 2.

 2.1- ( α ) Representa el nivel de significación o nivel de error que podría cometerse. Si fuésemos a ubicarlo en el gráfico representaría todos los valores que quedan debajo de la curva, pero fuera del intervalo de confianza.

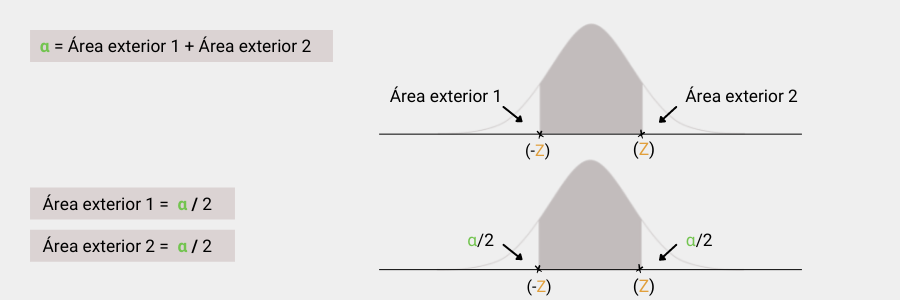
La forma de calcular α es bastante simple: α = 1 - valor de la confianza, ya que 1 representa todo el valor bajo la curva.

Por su parte, el valor de la confianza es un porcentaje expresado decimalmente. Su valor dependerá del nivel de especificidad que necesitemos. Si deseamos obtener mayor especificidad en los datos, debemos usar un porcentaje lo más cercano posible a 100. Por lo general, se suelen usar porcentajes entre el 95 % (0.95) y el 100 % (1.00).

Una vez calculado el valor de α debemos localizar el valor de Z que corresponde al valor de α/2. Nota que α se divide entre dos porque los puntos Z están a la misma distancia del centro del gráfico y, por tanto, dejan fuera de sí iguales valores de α.

Podemos utilizar la tabla de acumulado complementario (tabla matemática que se utiliza para mostrar la probabilidad de que un suceso estadístico sea mayor que Z) y unir los valores de la primera columna con la primera fila para formar el valor de Z como muestra el gráfico.

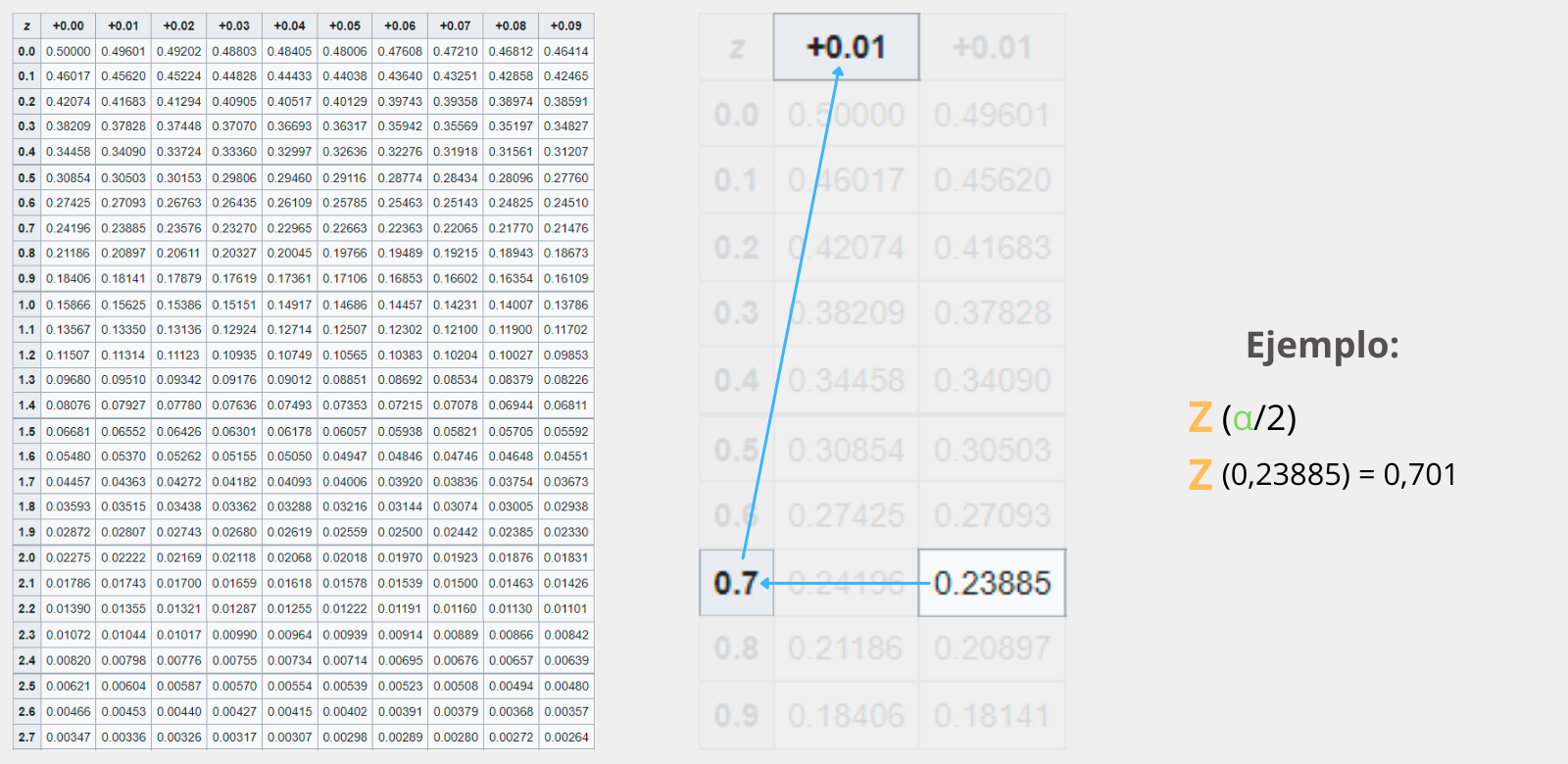
 3.0- ( S ) Representa la desviación estándar. Para un conjunto de datos su fórmula depende de si la estamos calculando para un total de datos, o para una muestra.

 Para un total de datos:

S = √ Σ(x - x̅)² / n

 Para una muestra de datos:

S = √ Σ(x - x̅)² / (n - 1)

 En ambas fórmulas Σ representa «suma de», x representa a cada uno de los datos y n es la cantidad de datos analizados. Comprenderás mejor el cálculo de S con el desarrollo del ejemplo.

 Analicemos un ejemplo

Supongamos que vamos a calcular el intervalo de confianza para el conjunto de datos: 13, 4, 35; tomando en cuenta un valor de confianza del 95 %.

Paso 1: Planteamos la fórmula de intervalo de confianza.

<M> _1-α = x̅ ± Z_α/2 * S / √(n) 

Paso 2: Calculamos la media o promedio.

x̅ = (13 + 4 + 35) / 3

x̅ = 17.33 

Paso 3: Calculamos α tomando en cuenta que el valor de confianza es de 95 % o 0.95.

α = 1 – 0.95

α = 0.05

 Paso 4: Calculamos Z _α/2.

Z_{0,05 / 2}

Z_0,025 = 1.96

 Paso 5: Calculamos S utilizando la fórmula para el total de datos, pues no estamos utilizando una muestra.

 S = √ Σ(x - x̅)² / n

S = √Σ(13 – 17.33)² + (4 – 17.33)² + (35 – 17.33)² / 7

S = √18.7489 + 177.6889 + 312.2289 / 7

S = √508.6667 / 7

S = 22.5536 / 7

S = 3.22

 Paso 6: Sustituimos los valores en la fórmula inicial de intervalo de confianza y calculamos.

<M> _1-α = x̅ ± Z_α/2 * (S / √n)

<M> _1-α = 17.33 ± 1.96 * (3.22 / √3)

<M> _1-α = 17.33 ± 1.96 * (2.23)

<M> _1-α = 17.33 ± 4.37[1] 

<M> _1-α = (17.33 – 4.37) ; (17.33 + 4.37)

<M> _1-α = 12.96 ; 16.7

 El valor del intervalo de confianza para el conjunto de datos: 13, 4, 35 y tomando en cuenta un valor de confianza del 95 % es de 12.96 a 16.7. 

En la práctica

Si quisiéramos obtener el intervalo de confianza al 90 % de una media de 4.9. El dato representa la media de las calificaciones de 25 alumnos que han sido tomados como muestra del total de alumnos de una escuela. Datos de cursos anteriores revelan que la desviación típica de las puntuaciones es de 2.01 puntos.

 Paso 1: Planteamos la fórmula de intervalo de confianza.

<M> _1-α = x̅ ± Z_α/2 * (S / √n)

 Paso 2: Identificamos cada uno de los datos que poseemos y calculamos todos cuantos podamos a partir de ellos.

 x̅ = 4.9

n = 25

S = 2.01

Valor de la confianza = 0.90

α = 1 - 0.90

α = 0.1 

Z (α / 2) = 1 - 0.90

Z (0.1 / 2) = 0.05

Z (0.05) = 1.64 (según tabla de acumulado complementario)

Paso 3: Sustituimos los valores en nuestra fórmula y calculamos.

<M> _1-α = 4.9 ± 1.64 * (2.01 / √25)

<M> _1-α = 4.9 ± 1.64 * (2.01 / 5)

<M> _1-α = 4.9 ± 1.64 * 0.402

<M> _1-α = 4.9 ± 0.659

<M> _1-α = (4.9 – 0.659) ; (4.9 + 0.659)

<M> _1-α = 4.24 ; 5.55 

El intervalo de confianza de la media de notas de los alumnos se sitúa entre 4.24 y 5.55 puntos.



¿Cómo calcular? es una columna para contribuir a la educación ciudadana en temas de datos, estadística y matemática práctica en la vida cotidiana. Puedes leer aquí todos los textos publicados.