¿En qué medida puede un suceso ocurrir, o no? Aunque no seamos conscientes de ello, la mayor parte de nuestras acciones están vinculadas a esta pregunta. Cada decisión que tomamos está vinculada a nuestra experiencia y a un cálculo mental de probabilidades.
Al cruzar la calle tomamos precauciones porque sabemos que con alguna probabilidad pueda ocurrir un accidente; o al cocinar podemos ponerle una pizca más de sal a nuestra elaboración porque es probable que la necesite. Pero ¿qué sucede cuando queremos calcular de forma numérica la probabilidad de que algo suceda?
Compartimos algunos consejos para que puedas calcular de forma fácil la probabilidad en situaciones comunes.
Puntos de partida
La probabilidad se estudia como una rama de las matemáticas y comprende el análisis de eventos aleatorios y experimentos. Aparte de las clásicas áreas de la física, la matemática y la filosofía, también se aplica de manera más aterrizada a las finanzas, las investigaciones médicas, la economía y los estudios sociales.
En general, existen dos grandes puntos de vista sobre la naturaleza fundamental de la probabilidad: el objetivo y el subjetivo. El primero se basa en la recolección de datos y asignación de números para describir algún estado de las cosas, los objetos o situaciones; mientras que el segundo se apoya en el sentido común y experiencia de las personas, aunque también asigna valores pero basados en un grado de creencia.
Algunas formas de calcularla
Las situaciones que analizaremos se enmarcan en el estudio objetivo de un fenómeno con datos concretos.
Regla de Laplace
Como imaginarás, la regla de Laplace se nombra así en honor a su creador Pierre Simon de Laplace (1749-1827). Se utiliza para calcular probabilidades en elementos equiprobables; es decir, son eventos en los cuales se puede obtener solo un valor y en los que todos los elementos tienen igual número de probabilidad de salir si elegimos uno al azar.
La fórmula para calcular la probabilidad en estos casos es la siguiente:

P(A): Probabilidad de que ocurra el evento A.
⦁ Número de casos favorables: Representa la cantidad de casos en los que puede ocurrir A.
⦁ Número de resultados posibles: Representa la cantidad de resultados totales que podemos obtener.
Veamos un ejemplo. ¿Qué probabilidad hay de que si lanzamos un dado obtengamos el número tres en la cara superior del dado? Planteamos la fórmula anterior y calculamos de la siguiente manera:

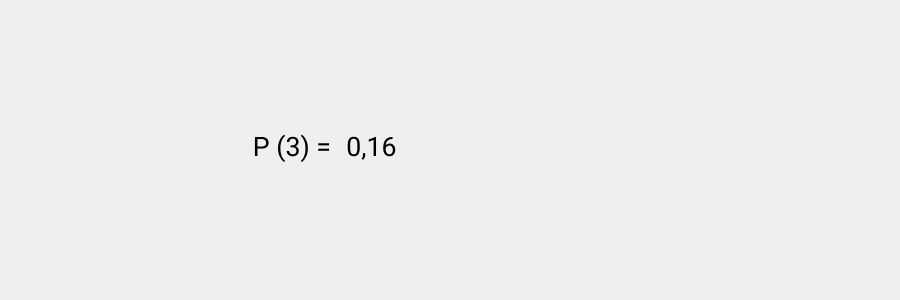
Si quisiéramos calcular qué probabilidad existe de que salga 3 o 4 podemos hacerlo realizando la misma fórmula. En este caso el evento continúa siendo de elementos equiprobables, pues solo puede salir uno de los dos en cada lanzamiento del dado y cada cara tiene la misma cantidad de probabilidades que el resto de resultar la ganadora.
Nota: Fíjate cómo hemos empleado el signo U, el cual indica la probabilidad de que ocurra el evento 1 (obtener un tres en la cara superior) o el evento dos (obtener un cuatro en la cara superior). Es importante que comprendas este punto pues lo necesitaremos más adelante.

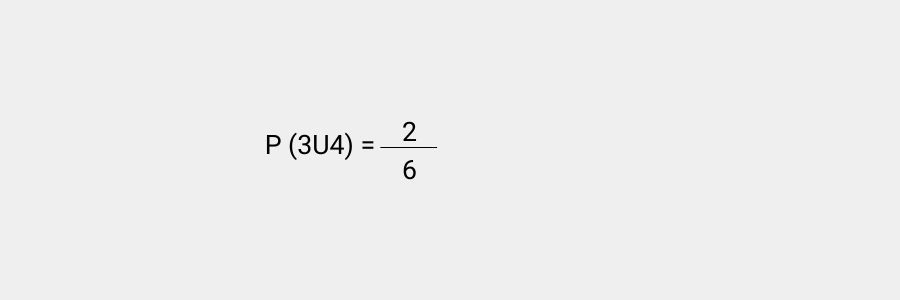

Calcular probabilidades con regla de sumatorias
Con la forma de cálculo anterior podemos estimar las probabilidades de lanzamientos de dados, lanzamientos de monedas y eventos equiprobables como la probabilidad de que un alumno que pese menos de 50 kilogramos sea elegido al azar entre un grupo de 30 alumnos. Pero ¿qué sucede cuando dos eventos pueden cumplir las condiciones de probabilidad al mismo tiempo?
Imaginemos que deseamos estimar la probabilidad de que, en un grupo de figuras geométricas, sea elegido al azar un triángulo o una figura de color amarillo (sea triángulo o no).
En estos casos, la probabilidad se calcula empleando otro método que, aunque es un poco más complicado que el anterior, parte de él. Para ayudarte a comprenderlo de manera sencilla desarrollaremos el ejemplo anterior. Luego podrás adecuar esta lógica a situaciones reales.
Supongamos que poseemos 12 figuras dispuestas de la siguiente forma:

Si quisiéramos calcular la probabilidad de que, al elegir una figura al azar, la figura sea un triángulo o una figura amarilla, la regla de Laplace no aplica; pues no serían elementos equiprobables, ya que la probabilidad se cumpliría tanto si obtenemos un triángulo, una figura amarilla o un triángulo amarillo.
Para realizar el cálculo debemos reorganizar nuestras figuras en dos conjuntos: el de los triángulos (A) y el de las figuras amarillas (B).
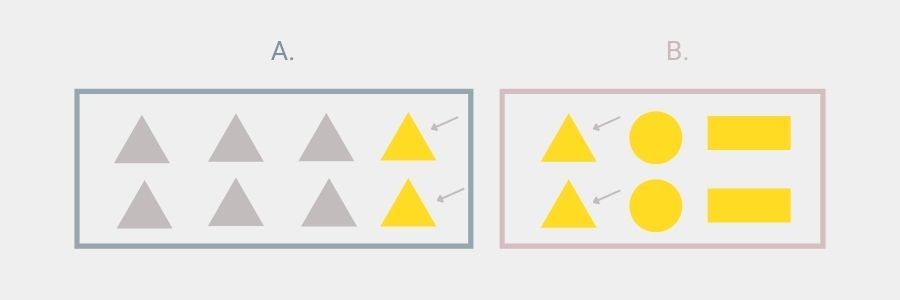
Nota como hay triángulos amarillos que se repiten en ambos conjuntos, ya que pertenecen a ambos conjuntos. Visto de esta forma pudiera dar la idea de que el total de figuras es 14, cuando realmente es 12. A partir de esta posible distorsión recomendamos representarlo visualmente de la siguiente forma:
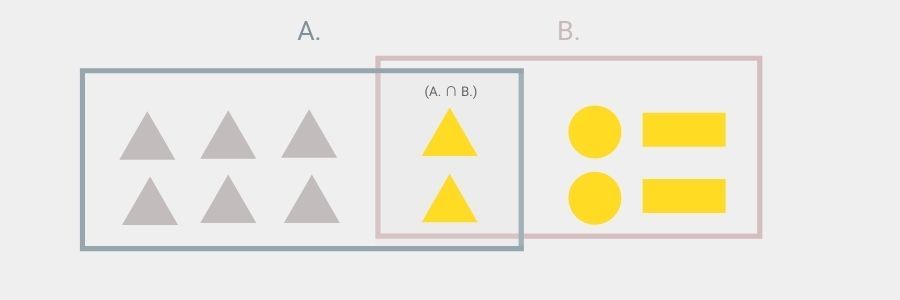
A la izquierda y con un recuadro azul tenemos el conjunto A, el cual engloba todos los triángulos. A la derecha y con un recuadro roza está el conjunto B, que engloba todas las figuras amarillas incluidos los dos triángulos amarillos que también pertenecen a A.
Debido a la condición de que ambos conjuntos comparten ciertos elementos, la fórmula de la adición para calcular probabilidades propone:
⦁ Calcular las probabilidades individuales de cada conjunto.
⦁ Sumarlas entre sí.
⦁ Sustraerles la probabilidad individual de los elementos compartidos entre ambos conjuntos.
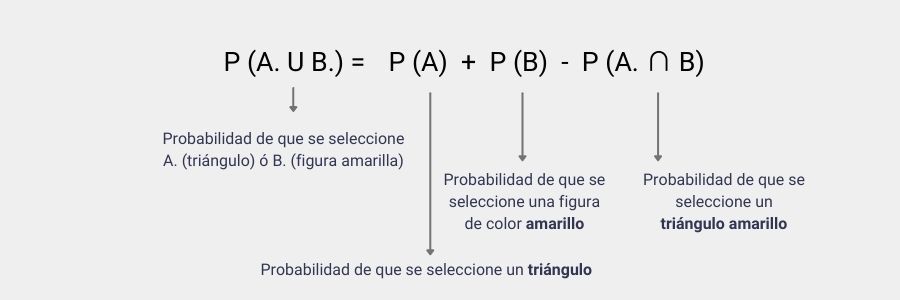
Nota: Fíjate cómo el signo U indica probabilidad de A o B, mientras que el signo ∩ indica que se cumplen ambos, A y B.
Para calcular P(A) procedemos con la fórmula Laplace analizada anteriormente. En este ejemplo, el número de casos favorables coincide con la cantidad de triángulos, y el número de resultados posibles coincidiría con el número total de figuras; ya que al realizar la selección al azar pudiera elegirse cualquiera de ellas.
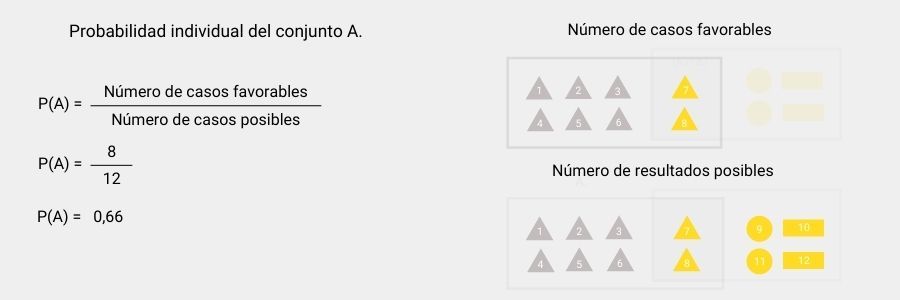
Una vez calculada la probabilidad individual del conjunto A, procedemos a calcular P(B) empleando el mismo método. El número de casos favorables coincide con la cantidad de figuras amarillas, mientras que el número de resultados posibles vuelve a ser la cantidad total de figuras.
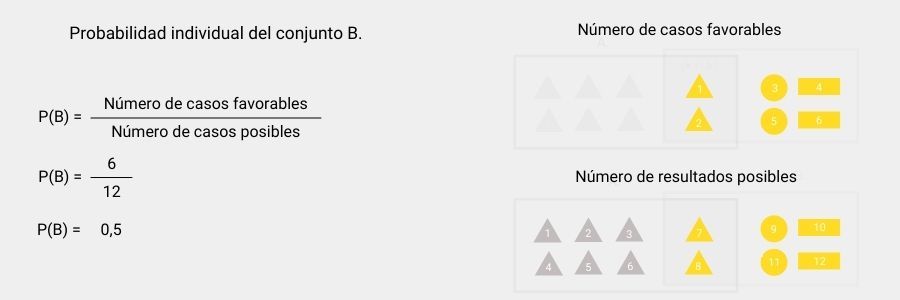
Para calcular los elementos que se repiten en ambos conjuntos P(A∩B), emplearemos también la fórmula de Laplace. El número de casos favorables sería el número de triángulos amarillos y el número de resultados posibles sería el total de figuras.
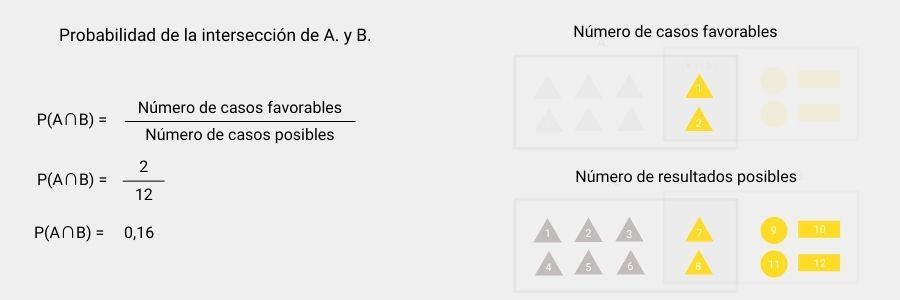
Una vez calculadas todas las probabilidades individuales podemos integrarlas a la fórmula y calcular la probabilidad de que, al seleccionar una figura del total, esta sea un triángulo o una figura de color amarillo.
En este cálculo de probabilidades los resultados siempre oscilarán entre las cifras 0 y 1, en el que 0 es la menor probabilidad de que algo ocurra y 1 la máxima. Es por ello que en el caso analizado la probabilidad de que al elegir una figura sea un triángulo o una figura amarilla es total, no existe probabilidad de que ocurra algo diferente.
¿Cómo aplicar estas fórmulas en la vida diaria?
Para explicar de manera sencilla cómo calcular probabilidades, veamos un ejemplo práctico que puedes emplear en la vida cotidiana.
Todo pequeño negocio calcula las probabilidades de ventas de sus productos o servicios. Solo debe comenzar a tomar datos de sus ventas diarias y de la cantidad de clientes que lo visitan.
Supongamos que una pizzería desea hacer una oferta de un pack de dos pizzas (margarita y jamón) por un precio especial. Para ello desea conocer la probabilidad de que ambas le gusten a un mismo cliente.
Conociendo los porcentajes de clientes que consumen pizza margarita, pizza de jamón y el porcentaje de clientes a los que le gustan una de las dos, pudieran calcular a qué porcentaje de clientes probablemente le guste ambas pizzas juntas.
Para el desarrollo de este ejemplo empleamos los siguientes datos:
Pizza margarita: 65 %
Pizza de jamón: 70 %
Pizza margarita o de jamón: 80 %
Pizza margarita y de jamón: ¿X?
Una vez definidos los datos calculamos utilizando la regla de sumatorias:
P(margaritaUjamón) = P(margarita) + P(jamón) - P(margarita∩jamón)
80 % = 65 % + 70 % - P(margarita∩jamón)
80 % + P(margarita∩jamón) = 65 % + 70 %
P(margarita∩jamón) = 65 % + 70 % - 80 %
P(margarita∩jamón) = 55 %
Con lo cual, la probabilidad de que a un cliente le gusten ambas pizzas es de un 55 %. Probablemente sea una buena idea para este negocio hacer una oferta como la que planean.
Probablemente útil
El cálculo de probabilidades puede llegar a ser complicado en función de su objeto de estudio. No obstante, hemos podido comprobar cómo con fórmulas sencillas se obtienen resultados que facilitan la toma de decisiones.
El principal factor a tener en cuenta para estos cálculos es identificar correctamente los elementos de las fórmulas analizadas. Para ello, recomendamos realizar el siguiente análisis antes de plantear la fórmula:
- ¿Tienen todos los elementos igual probabilidad? Si la respuesta es sí, probablemente puedas calcularlo con la regla de Laplace.
- ¿Existe la posibilidad de que más de un elemento cumpla las condiciones de la probabilidad? Si la respuesta es afirmativa, podrías separar los conjuntos de probabilidades y emplear la regla de sumatoria.
Recuerda que en el miembro izquierdo colocamos la probabilidad de que ocurra uno u otro (U). Mientras que en el miembro derecho se ubican las probabilidades individuales de los conjuntos y la probabilidad de que ocurran ambos (∩).
¿Cómo calcular? es una columna para contribuir a la educación ciudadana en temas de datos, estadística y matemática práctica en la vida cotidiana. Puedes leer aquí todos los textos publicados.











Comentarios
En este sitio moderamos los comentarios. Si quiere conocer más detalles, lea nuestra Política de Privacidad.
Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *